Astro 103 - Lecture 8

 Lectures Lectures  |
Lecture page |
|

 Lectures Lectures  |
Lecture page |
|
Giants
Super Giants
White dwarfs
Spectral types: O B A F G K M
 cool
cool
- temperature
SO?
(ii) deduce spectral type from spectrum
(iii) infer luminosity (L) from spectral type
(iv) infer distance (d) from apparent brightness
and luminosity
 d2 )
d2 )
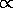 L/d2
L/d2 and then re-arrange terms and take the square-root:


- to a few Mpc (maybe!) from HST
 L/d2
L/d2
so,
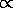
 =
= 
and
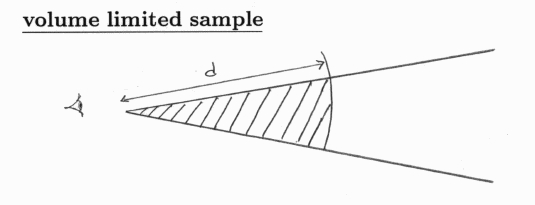
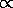 d3
d3
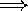
volume 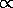 (
(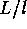 )3/2
)3/2
 brightness-limited samples
biased to bright objects
brightness-limited samples
biased to bright objects
 T4
T4
 R2):
R2):
 R2
R2
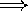 Total
luminosity of a spherical blackbody is proportional to the energy
times the area:
Total
luminosity of a spherical blackbody is proportional to the energy
times the area:
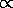 E * A
E * A so
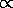 T4 * R2
T4 * R2 or

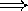 R
R
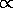 Mass4
Mass4
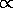 M3
M3
In reality the index is between 3 and 4, higher at higher masses.
The best 'average' value is 3.2, but we will stick with 4 for simplicity.
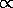 Radius2
Radius2When is this formula valid?
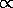 Mass0.7
Mass0.7
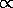 Radius5.7
Radius5.7... for the Main Sequence ONLY.
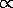 Mass/Luminosity
Mass/Luminosity 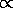 Mass-3
Mass-3
| Mass (Solar units) |
Luminosity (Solar units) |
Lifetime |
| 0.1 | ||
| 1 | 1 | 10 Gyr |
| 10 | ||
| 100 |
(b) not possible to estimate
(c) the bigger star is brighter in proportion to its greater mass
(d) the bigger star is brighter by a factor of 4, in proportion to its greater surface-area
(e) the bigger star is brighter by a factor of 6, in proportion to its greater volume
(b) twice as short as the Sun
(c) the same time
(d) indefinitely
(e) 8 times shorter than the sun
 Lectures Lectures  |
Lecture page |
|