1. Space Motions

apparent vs. space motion

proper motion is a tangential apparent motion:

- tangential to what?

- angular motion

- measured with respect to other stars

- typical proper motions are < 1 arcsec per year

tangential space motion = proper motion * distance

radial motion

- measured from the doppler shift of a spectral line

proper motion, distance, and radial motion

3 dimensional

space motion (km/s)

typical space motions are of order 10-100 km/s

2. Distances via Stellar Parallax

Use the Earth's orbit around the sun as baseline for triangulation:

Baseline = 2 A.U. (Earth's orbit)

Formula (just simple geometry using the small-angle approximation):

distance (parsecs) = 1 / angle (arcseconds)

the 'angle' is referred to as the 'parallax'

parsec = 3.26 light-years

arcsecond = arcminute

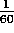arcminute 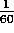= degree

Nearest star: Proxima Centauri 1.3 parsecs

- actually a 3-star system, one like the Sun

- visible to the eye

Next closest: Barnard's star 1.8 parsecs

- invisible to the naked eye

Inference:

Stars must come in a wide range of luminosity

Could space be filled with dim stars that we just can't see?

Limitation of parallax:

- difficult to measure parallax angle for objects more than a few parsecs away from the ground.

- European space-based observatories (Hipparcos and now Gaia satellelites) are revolutionizing the field, pushing geometric parallax measurements now to kpc distance-scales.

Remember the importance of parallax:

- primary measurement of distance in astronomy.

- the 'bottom rung' of the cosmic distance ladder.

- with parallax, we calibrate all other methods of determining distances to objects that are farther away.

3. Luminosity, Apparent Brightness, and Absolute Brightness

Inverse Square law - again!

Apparent brightness , l ...

... is the amount of light (radiation) that you see from an object when ...

... the object is at some distance d

... the object has some luminosity, L.

(luminosity = total energy given off in all directions per unit time)

Recall the inverse square law for gravity:

The surface of a sphere is proportional to it's radius r

The larger r, the bigger the area, the more the force (or here, light) has to be distributed, or diluted.

Think of a sphere of radius r = d

Then,

l = L / 4 d²

Absolute brightness is the apparent brightness of the object if it were placed at a distance d = 10 parsecs from the observer.

Think of 'absolute brightness' as a standard of reference.

There is nothing magical about 10 pc --

-- just an arbitrary choice.

4. Stellar temperatures and luminosities

Temperatures and luminosities of stars are observed to be highly correlated

The Hertzsprung-Russell diagram (1911-1913)

"HR diagram"

The Main Sequence

temperature and luminosity are correlated

Giants

more luminous (and larger size) than Main Sequence stars of same temperature

Super Giants

even more extreme than giants

White Dwarfs

very small, hot, and faint

How are they all related?

An evolutionary sequence? Sequences?

NB:

Don't confuse white dwarfs with luminosity class V ``dwarfs.''

They are NOT the same!

Red dwarfs are the cool-end of the Main Sequence, i.e. luminosity class V, and are NOT the same as white dwarfs.

Spectral types:

O B A F G K M

hot cool

"oh be a fine gorilla: kiss me"

"oblique bats announce: frigid grapes kill mice"

Each 'spectral type' has unique characteristic spectrum

Each is broken down into 10 subtypes, e.g. G0, .... G9

Each of these is broken down into 5 luminosity classes:

I, II super-giants

III giants

IV sub-giants

V ``dwarfs'' (the MAIN SEQUENCE)

The Sun is a G2 V star

Spectral Type	Temperature (degrees Kelvin)	"Color"
O	30,000	blue/purple
B	20,000	blue
A	10,000	white
F	8,000	yellow/white
G	6,000	yellow
K	4,000	orange
M	3,000	red