Consistency of work integrals vs. imaginary component of nonadiabatic eigenvalues?

[joelongjiamian]

Hi all,

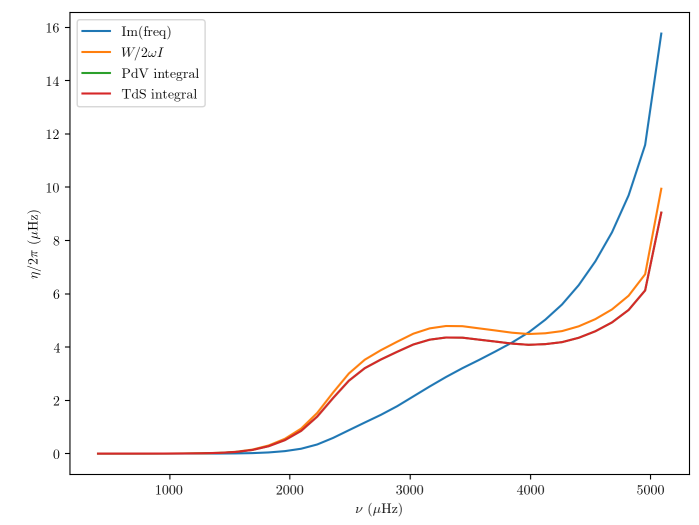
Has anyone tried determining damping rates from the eigenfunction work integrals? In particular, following Unno+ 1987 and/or Belkacem+ 2012 A&A 540, L7, we can cast the damping rate in terms of a work integral over the nonadiabatic eigenfunctions:



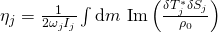
However, when I actually perform this computation, the values I get are not consistent with the imaginary components of the eigenvalues returned by GYRE:



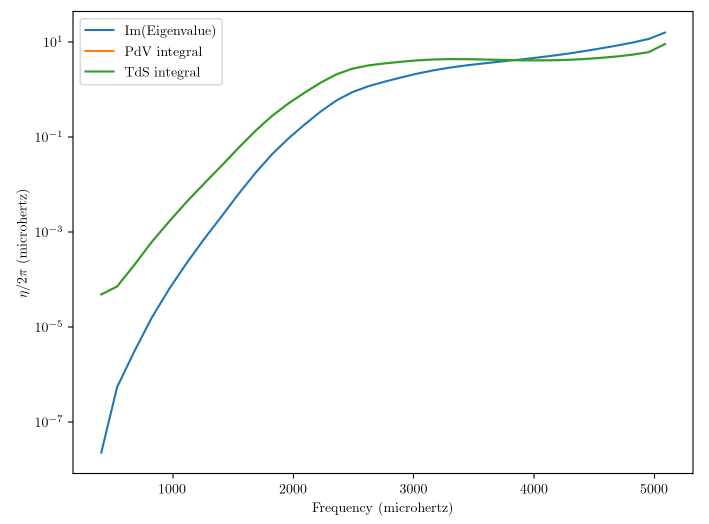
I should also clarify that this is with essentially a solar-calibrated model (as I'm mostly studying p-mode oscillations), so I don't really expect anything beyond radiative damping to come out of the calculation. Is this to be expected? That is, are the nonadiabatic eigenvalues returned from GYRE expected to be consistent with these integral damping rates?

[rhtownsend]

You're right that these two quantities should agree. A few questions:

1) What diff scheme are you using?
2) Are you evaluating the integral correctly?
3) Have you tried using GYRE's work integral (W in output items), which should give the same result as your integral?

cheers,

Rich

[joelongjiamian]

Hi Rich,

Thanks for the response.

2. and 3. I've checked my integrals against the values of W returned from the nonadiabatic calculation and they appear to be correct-ish — but the values of W also appear to not be consistent with the imaginary eigenvalue components:


There's a small scale difference between my integral and GYRE's W (invisible on a log plot, likely to be from differences in c_grav in GYRE vs. when I converted it to physical units in Python) but otherwise I'd say my work integral calculations are correct.

1. This plot was made for results returned from the Magnus GL2 scheme. I tried recomputing the eigensystem with the Magnus GL4 scheme (which gave work integrals that were even more inconsistent with the eigenvalues), Colloc GL4 (which did not manage to find all of the nonadiabatic eigenvalues), and Colloc GL2 (same result as above).

[rhtownsend]

Thanks for the update. There could be an issue with your model; could you post it (and your GYRE inlist) so I can have a look at it myself?

cheers,

Rich

[joelongjiamian]

Hi Rich,

Sorry for the delay. The model in question can be found here:

http://hyad.es/sendfile/payloads/Patched.GYRE

Namelist follows:

Code: Select all

&model
    model_type = 'EVOL'
    file = '../Patched.GYRE'
    file_format = 'MESA'
    ! file_format = 'FGONG'
    ! data_format = '(1P5E16.9,x)'
/

&constants
    G_GRAVITY = 6.67408d-8
/


&mode
    l = 0          ! Harmonic degree
/


&osc
    outer_bound = 'JCD'
    variables_set = 'JCD'
    inertia_norm = 'BOTH'
    !reduce_order = .FALSE.
    nonadiabatic = .true.
/

&num
    diff_scheme = 'COLLOC_GL2'
/

&scan
    grid_type = 'LINEAR'
    freq_min_units = 'UHZ'
    freq_max_units = 'UHZ'
    freq_min = 200
    freq_max = 5100
    n_freq = 1000
/

&grid
    alpha_osc = 15            ! At least alpha points per oscillatory wavelength
    alpha_exp = 9            ! At least alpha points per exponential 'wavelength'
    n_inner = 60                ! At least n points in the evanescent region
/

&nad_output
    summary_file = 'Patched-freqs-nad.dat'
    summary_file_format = 'TXT'
    summary_item_list = 'l,n_pg,n_p,n_g,freq,E_norm,W'
    freq_units = 'UHZ'
    mode_file_format = 'TXT' 
    mode_template = 'mode-nad.%J.txt'
    mode_item_list = 'M_star,R_star,l,n_pg,freq,W,dW_dx,x,xi_r,rho,P,T,Gamma_1,delta,nabla_ad,prop_type,eul_P,eul_rho,lag_rho,lag_P,lag_S,lag_T'
/

&ad_output
    summary_file = 'Patched-freqs.dat'
    summary_file_format = 'TXT'
    summary_item_list = 'l,n_pg,n_p,n_g,freq,E_norm'
    freq_units = 'UHZ'
    mode_file_format = 'TXT' 
    mode_template = 'mode.%J.txt'
    mode_item_list = 'M_star,R_star,l,n_pg,freq,x,xi_r,rho,P,T,Gamma_1,prop_type,eul_P,eul_rho,lag_rho,lag_P'
/

[rhtownsend]

Hi Joel --

I think I've tracked down the problem. There are a handful of bugs in GYRE 5.2 which manifest themselves when the JCD boundary conditions are used in non-adiabatic calculations, and/or when the JCD variables set is used in radial-mode non-adiabatic calculations. So, you were getting hit by both.

To fix the problem with 5.2, download and save the attached patch file to the $GYRE_DIR directory. Then, run the commands

Code: Select all

patch -p1 < nonad-bc-patch.diff 
make clean
make

This should help fix your issues. Let me know how you get on.

cheers,

Rich

nonad-bc-patch.diff

Patch for JCD vars/bc

(1.74 KiB) Downloaded 283 times

[joelongjiamian]

Hi Rich,

Here's what I get with the patch applied for COLLOC_GL2 (and also Magnus). These are the absolute values of the damping rates (there's a sign change at the large discontinuity). Still seeing issues with the work integrals (both mine and GYRE's) for the 4th-order difference schemes.

[rhtownsend]

Hi Rich,

Here's what I get with the patch applied for COLLOC_GL2 (and also Magnus). These are the absolute values of the damping rates (there's a sign change at the large discontinuity). Still seeing issues with the work integrals (both mine and GYRE's) for the 4th-order difference schemes.

Hi Joel --

Given the model, this plot is probably as good as you're going to get. What issues are you seeing with the 4th-order schemes? FYI, the eigenfunctions for the MAGNUS_GL4 scheme are known to be pretty ragged for non-adiabatic calculations.

cheers,

Rich

[joelongjiamian]

Hi Rich,

It is as you describe — the damping rates are very ragged (quite large variations of either sign). I can live with the second-order results for now. Thanks for your help!