Astro 1 - Lecture 21
Matthew A. Bershady
Department of Astronomy & Astrophysics
Penn State University
Fall 1996
This document may not be copied for sale
All Rights Reserved
© 1995 Matthew A. Bershady
 Lectures Lectures  |
Lecture page |
|
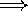 cool
cool  L/d2
L/d2 
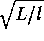
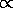 L/d2
L/d2 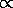
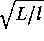 =
= 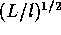
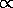 d3
d3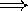
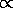 (
(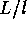 )3/2
)3/2 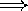 brightness-limited samples
biased to bright objects
brightness-limited samples
biased to bright objects 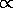 T4
T4 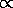 R2
R2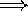 Total
luminosity of a spherical blackbody is proportional to the energy
times the area:
Total
luminosity of a spherical blackbody is proportional to the energy
times the area: 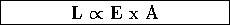
 T4 x R2
T4 x R2 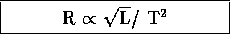
 R
R  Radius2
Radius2 Mass4
Mass4 Mass/Luminosity
Mass/Luminosity  Mass-3
Mass-3